The Metaphor
Some people like to rely on a serendipitous process when picking their next book. Perhaps a book with a nice cover or a book that they saw an interesting-looking-person reading at a book shop. Stranger still– I’ve known a man to pick a book off a rack simply because the edge of a shadow fell on it. All of these methods introduce a bit of randomness into the book selection process. We get stuck in the literary equivalent of a Pandora station that has grown a bit stale. And, of course, this doesn’t just apply to what books we read but to our thinking at large.
I prefer to use a stochastic process.
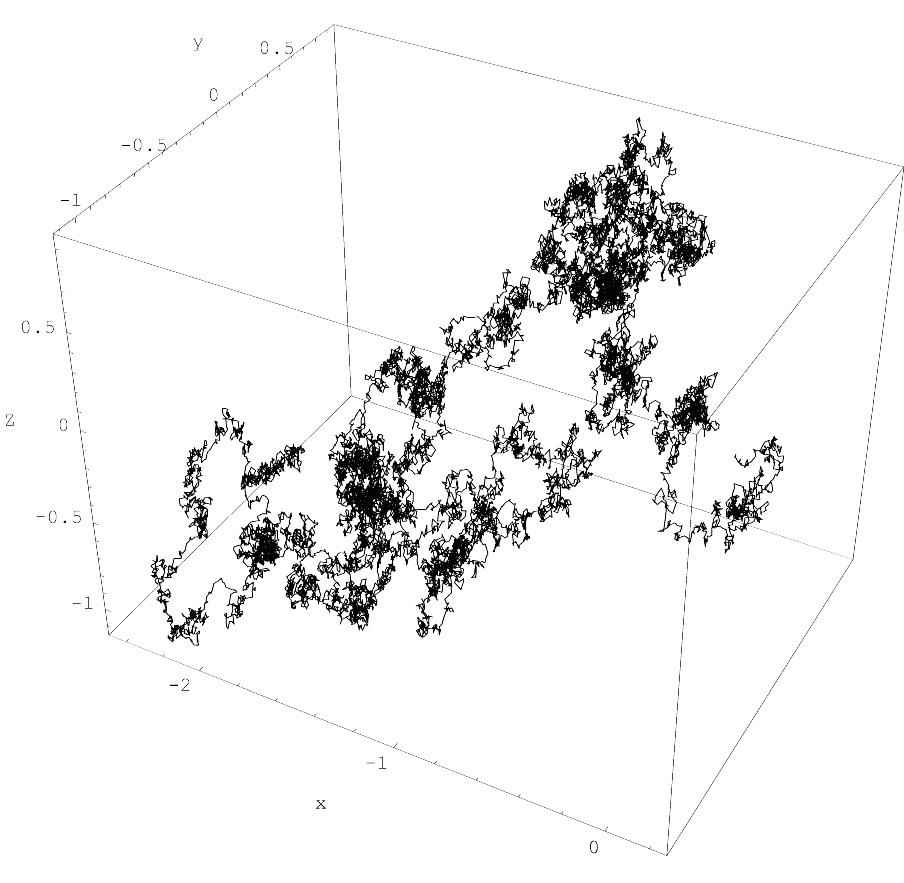
The wandering function in the image above is a specific type of stochastic process called Brownian Motion. This type of motion is how particles move about in a fluid. Brownian motion is simultaneously everywhere continuous and nowhere differentiable.
Everywhere continuous functions are the type of functions we are all used to and we all prefer. Roughly, continuous functions have no “tears”. If you were to draw the function, moving from one end to the other, you would never lift your hand.
Somehow, this notion is not at odds with the idea of nowhere differentiable. This is perhaps best visualized by imagining a fractal that, regardless of zoom level, will never be “smooth”.

The Universe somehow uses its finite mind to guide millions of particles along an endlessly complex path in the glass of water on your desk and in the air all around you.
This isn’t just another thegoldenmule tangent (wow, incredible calculus pun), it’s a vivid description of my study habits.
The Reality
I have directed study goals: specific books I want to read, exercises I want to complete, videos I want to watch, numbers of balls I want to be able to juggle at once (it’s four). These, I presume, will help me understand things I don’t currently understand “well enough”, or in the case of the juggling thing– will simply endear me to my children.
But there is a problem here.
Upon actually finishing the highly recommended Quantum Computing Since Democratus earlier this year (no big deal, it was pretty tough but I understood 100% of it, no big deal), I had a much longer reading list than I started with and completely different ideas about where I wanted to go. The same is true of just about every book I’ve ever read on just about any subject (with the exception of The Boxcar Children series). This is an endlessly deep endeavor for a simple mind like mine: the-mild-mannered-goldenmule is but a man.
I am shackled by limited intelligence, standing near the antipode of omniscience, staring up into space with drool on my chin– and there is really only one thing to do: exacerbate the problem.

I throw more particles into my pot of Brownian-research-stew. A Book of Bees (a beautiful guide to beekeeping), a 1950s textbook I found at Goodwill for elementary art educators [ref]“A work of art is not a product of nature; it is a product of human spirit, thinking, and emotions, and can only be understood when the driving forces which lead to its creation are understood.”[/ref], and Jack London’s classic: The Sea Wolf. I introduce more chaos as I read a chapter of each in rotation.
Scores have read Jack London– far fewer have read Jack London with art education and beekeeping on the mind. Perhaps no one but me has done it without being an actual beekeeper (suck on that, Gao Bingguo!).
In the intersection of these works (as described in the classic article on How Breadth Leads to More Interesting Specialization) are new ideas that can’t be formulated by your average $$y = mx + b$$ nonsense. Strange beasts arise from the bubbling, stochastic ooze.
Fie upon differentiable study!
I bite my thumb at linear learning!
My mind needs chaos to succeed! (and yours does too)